姓名：吴雨桥
学号：2013301020142
日期：2016年5月29日

对于波的运动，我们有波动方程

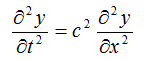
这个波动方程对于不同种类的波都是适用的，只需要把对x的求二次偏导相应修改一下即可。在本文中我只考虑一维弦上的波动。y代表弦上各点相对于其平衡位置的位移，x代表各点在弦上的坐标，t代表时间，c代表波在弦上的传播速度。
接下来我们考察初始时刻在弦上施加一个高斯型的干扰后，弦上波的传播情况。这里我们选择弦长为1m，c=300m/s，dx=0.01m，dt=dx/c。边界点固定。在弦上施加的干扰为

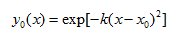
其中x0=0.3m，k=1000m^(-2)。弦上波的传播情况如下：

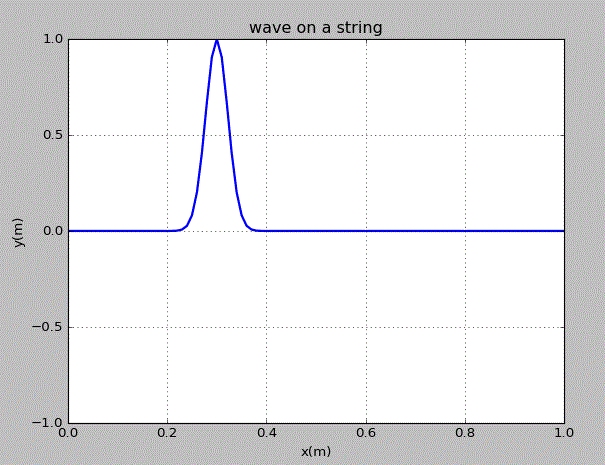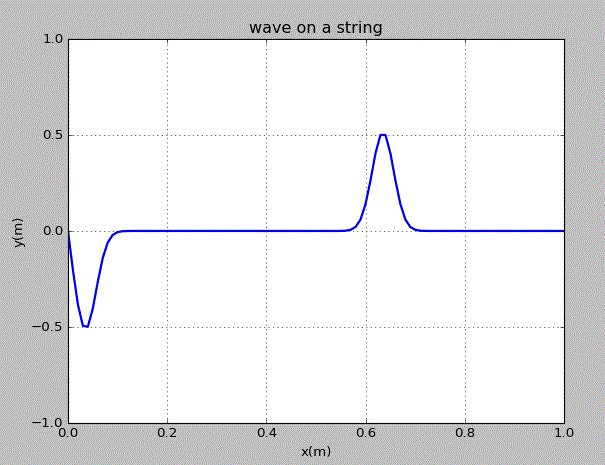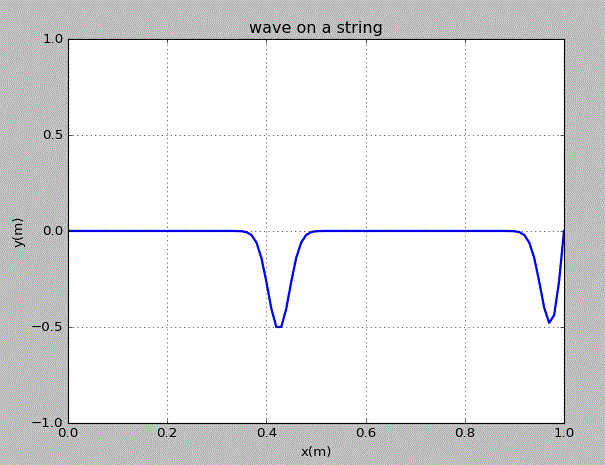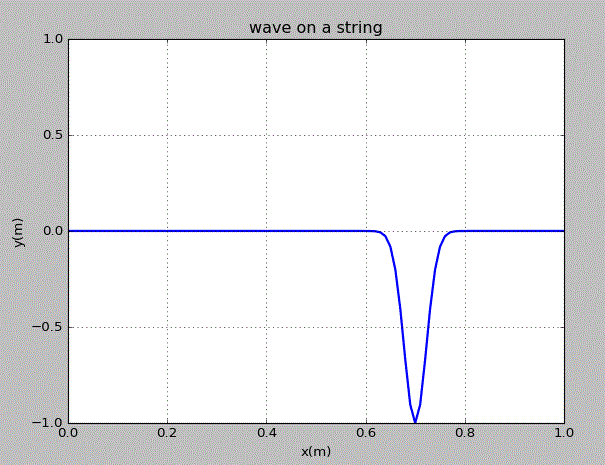
点击图片可获取绘图代码。由图可知，高斯型的干扰变为了两个相反方向的波传播，这两个波的峰值为原干扰的一半。且当其传播到了边界点时，波峰变为波谷，波谷变为波峰，这直接对应于物理中的半波损失，即波从光疏介质传播到光密介质时相位会减少180°。

齐次线性偏微分方程的一个重要特征是有限个解的线性组合也是方程的解。由此，在弦上运动的两个波包的运动是独立的。为了说明这一点，我们在弦上的x=0.3m，0.7m处各施加一个峰值不同的高斯型扰动，观察之后波包的运动。

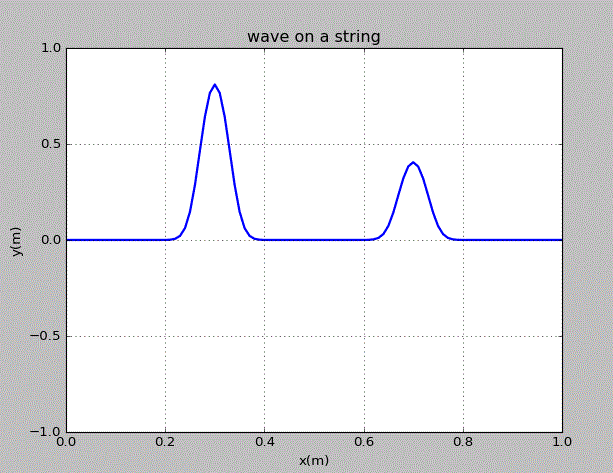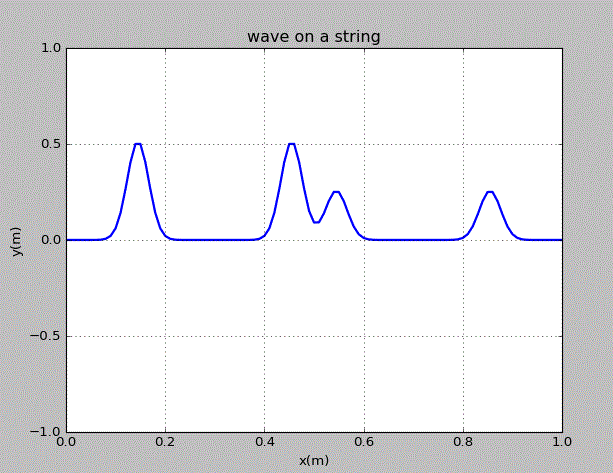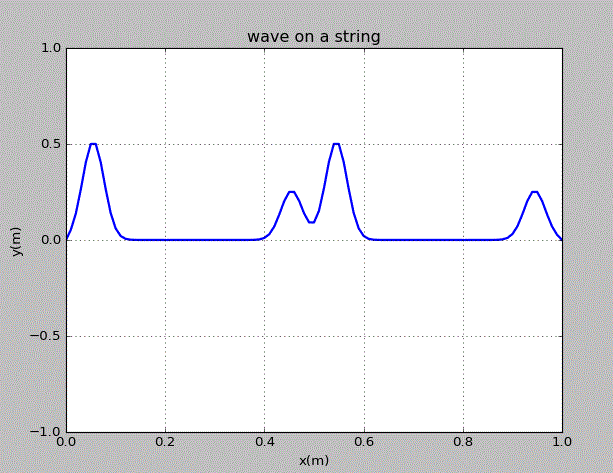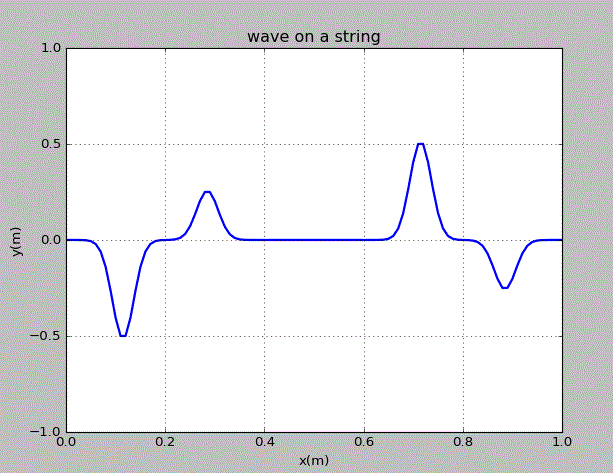
点击图片可以获得绘图代码。由图可知，各个波之间没有相互干扰，其在“碰撞”前后的形状和速度均没有变化。由此可知，这几个波作为弦的运动的解，是相互独立的。

接下来我们考察当初始波形不同时弦上的波的传播情况。
当初始的波为x=0.4~0.6上的方波时,情况为：

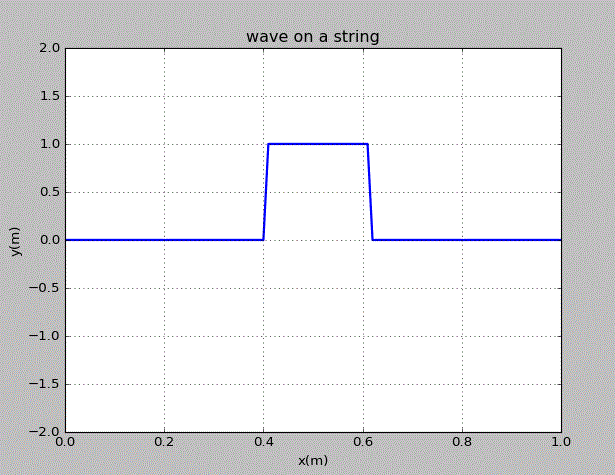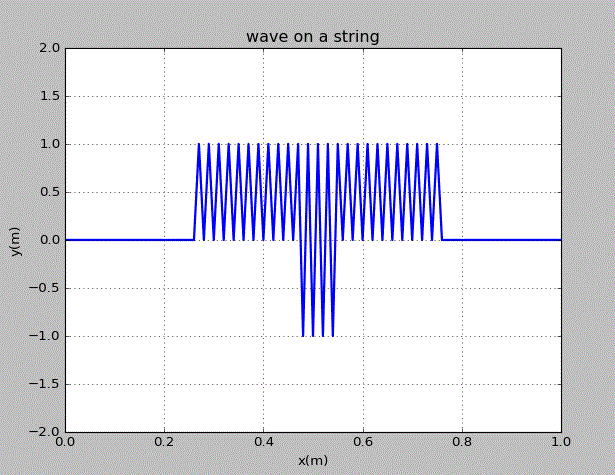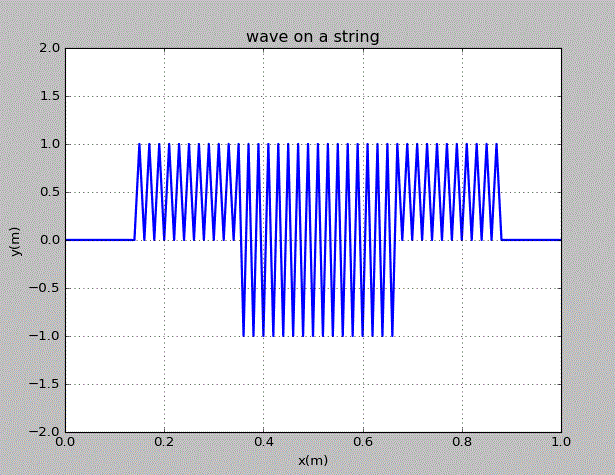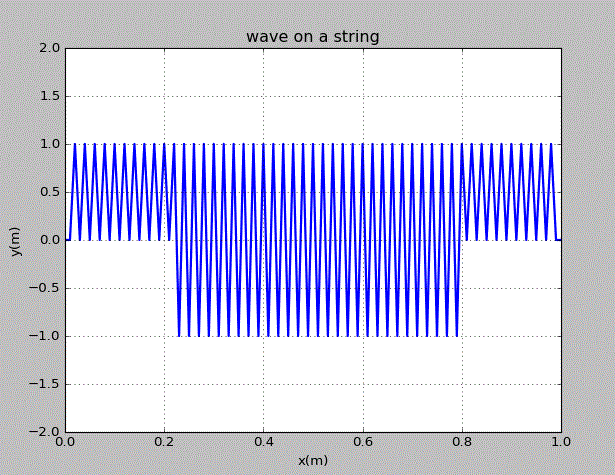
当初始的波为三角波时，情况为：

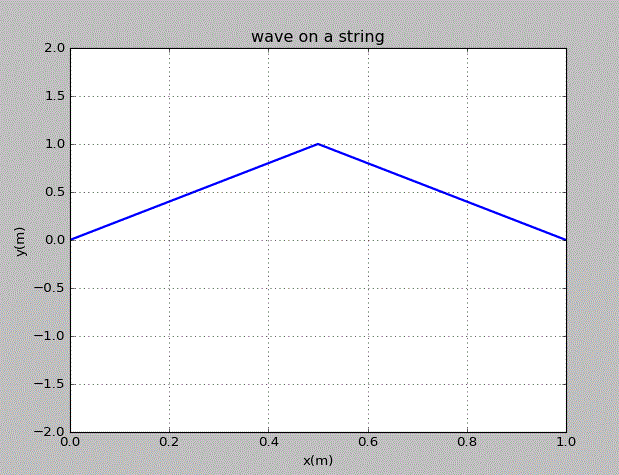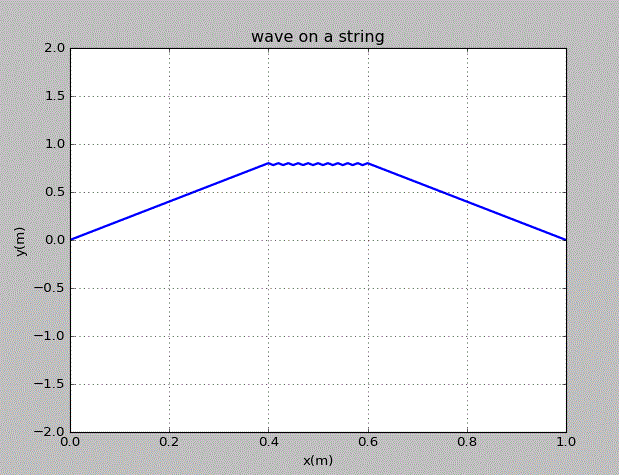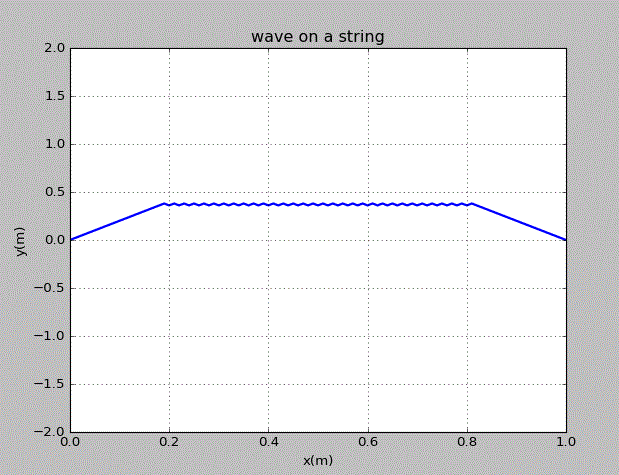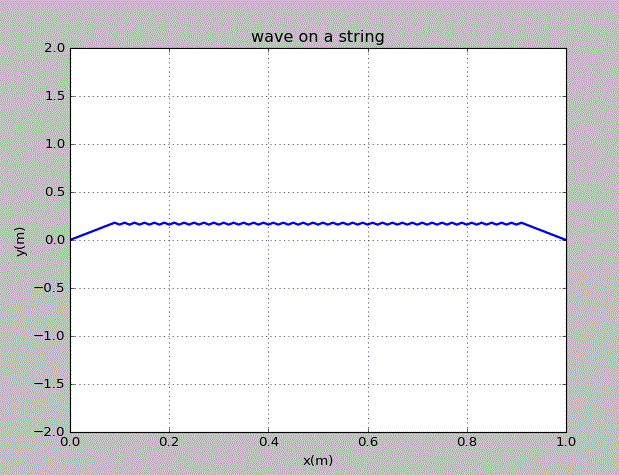
当初始的波为上半圆时，情况为：

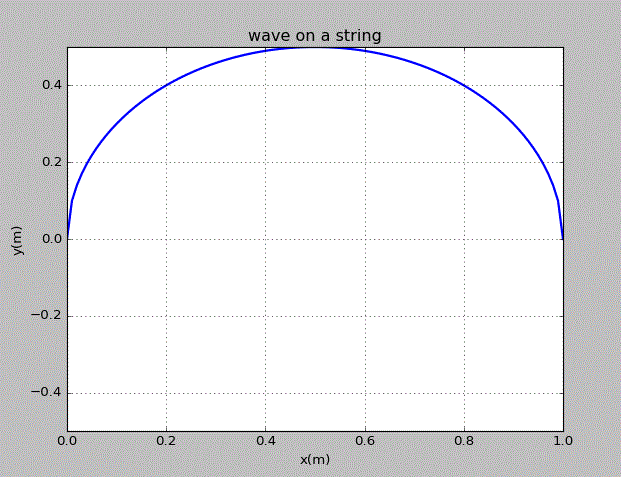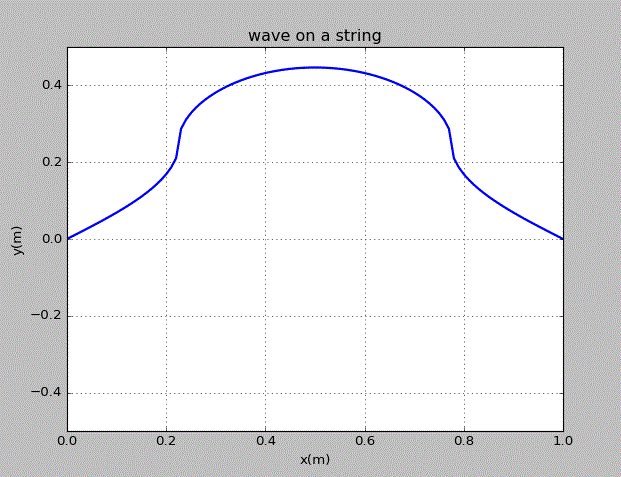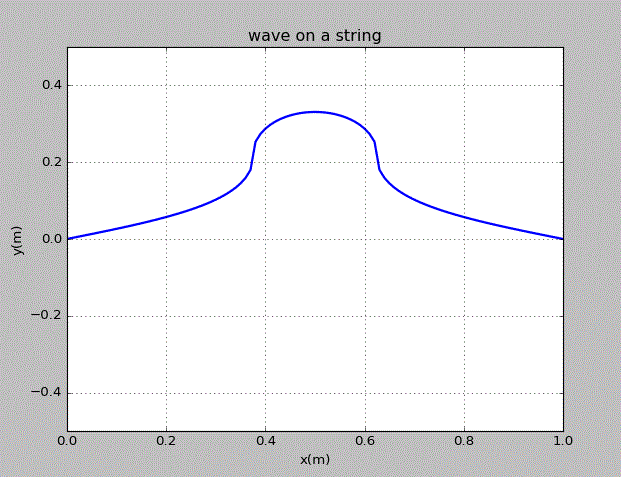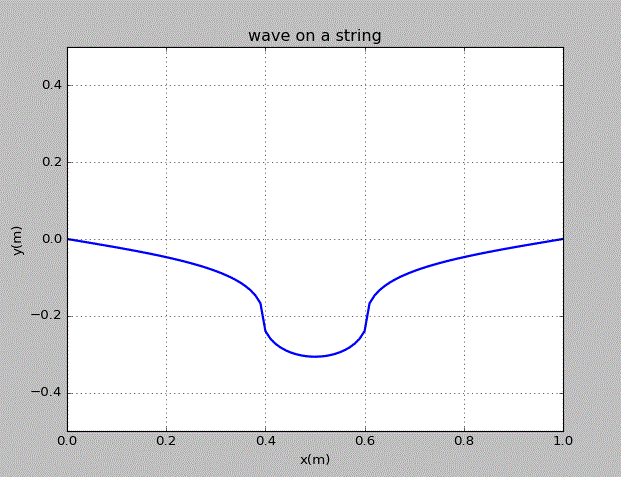
这里探究弦上的波的power spectrum。当在上文的弦的中心位置加上高斯型的扰动后，距离x=0处端点距离为弦长的5%的点的振动大小随时间的变化情况为：

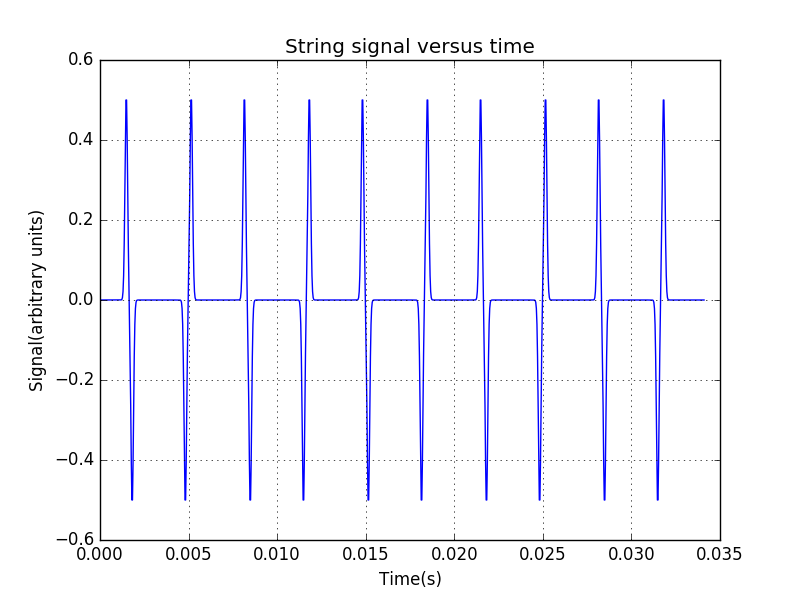
由此我们可以做出其power spectrum图。

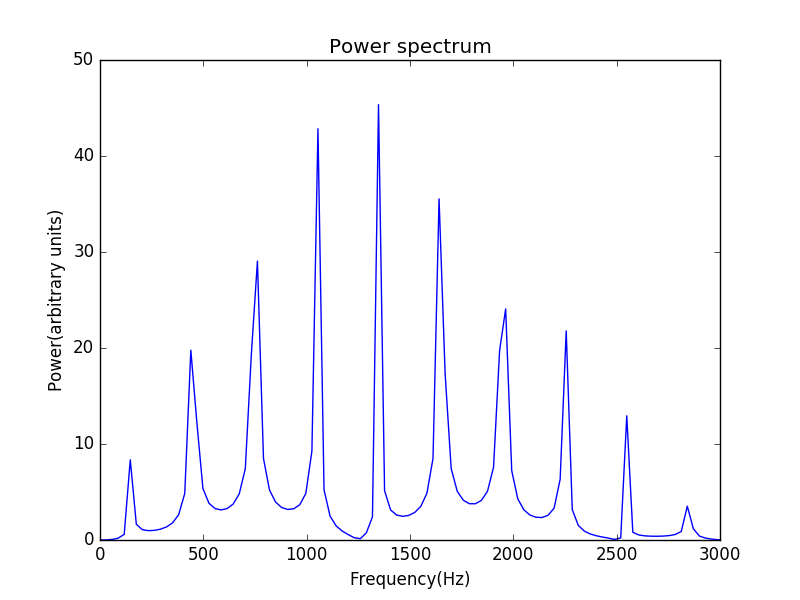
点击图片可以获得绘图代码。显然，power spectrum上当频率为150Hz的奇数倍时有峰值。
当扰动施加处稍稍偏离中心时，power spectrum为

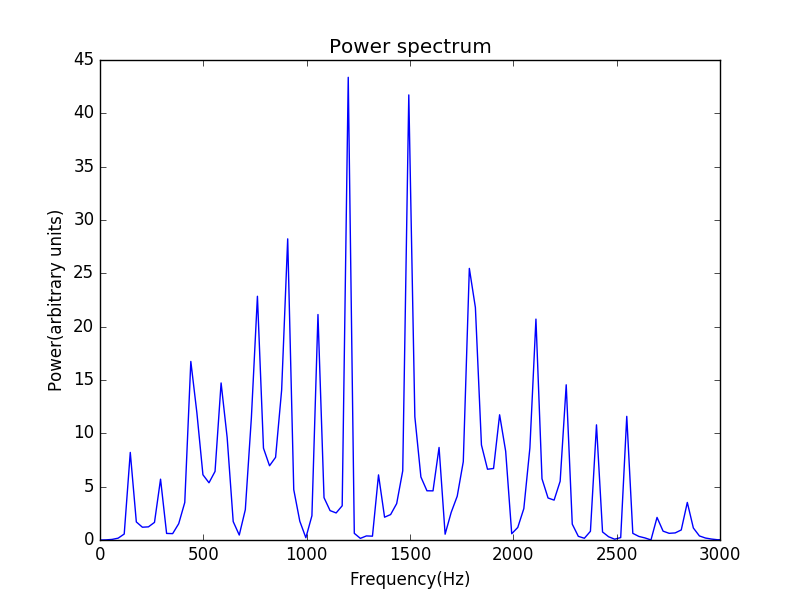
可见此时当频率为150的整数倍时就有峰值。

现在考察当初始波形为三角波的情况下的power spectrum。当三角形的上顶角对应的位置为弦的中心时，信号为

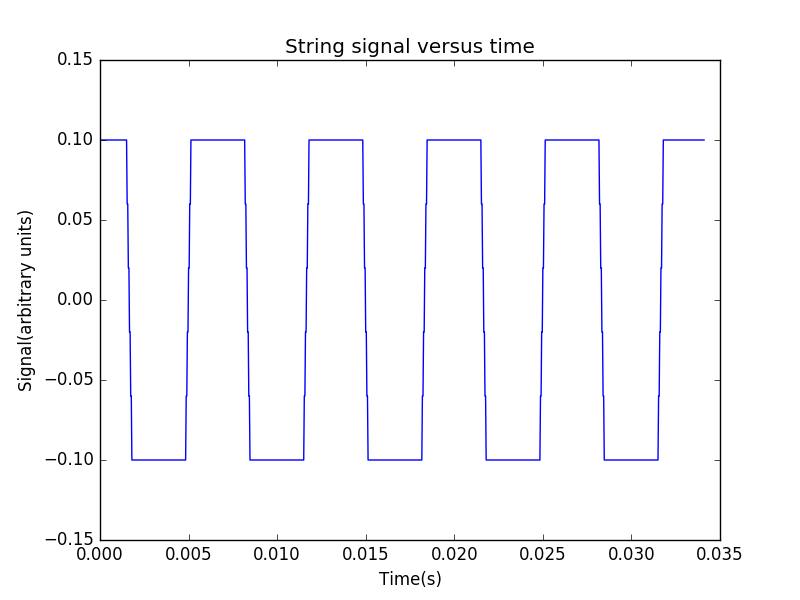
频谱为
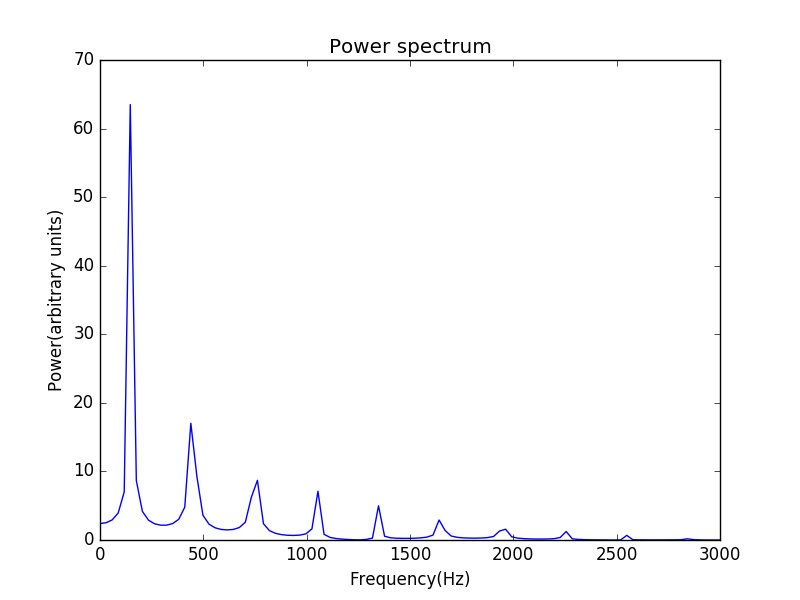
点击图片获得绘图代码。由图可见频率谱上有几个峰，随着频率的增大峰值在减小。
当上顶角位置偏离弦的中心时，信号为

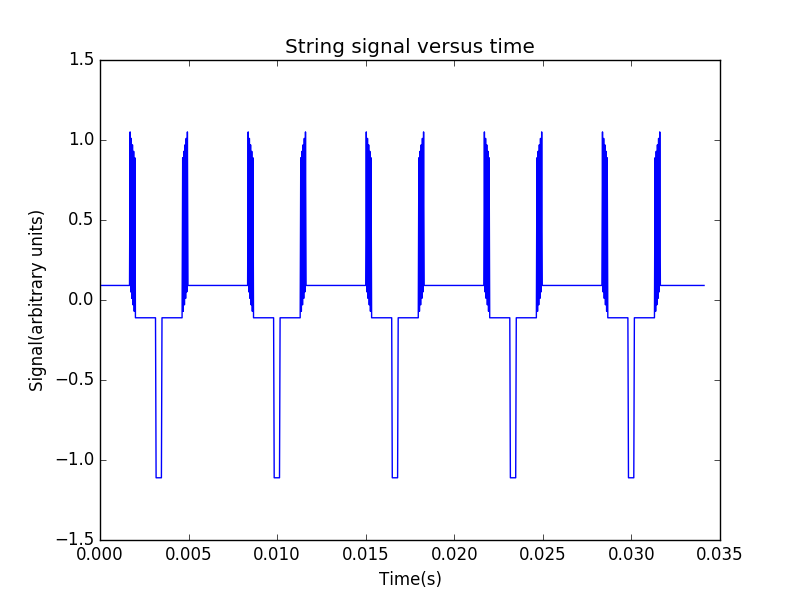
频谱为

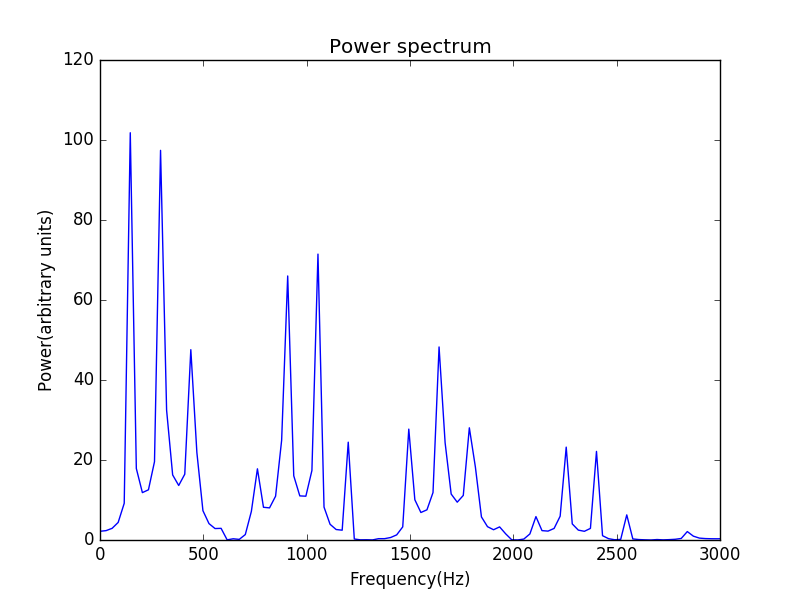
可见，由于初始的波形没有了对称性，频谱上多出了一些峰。